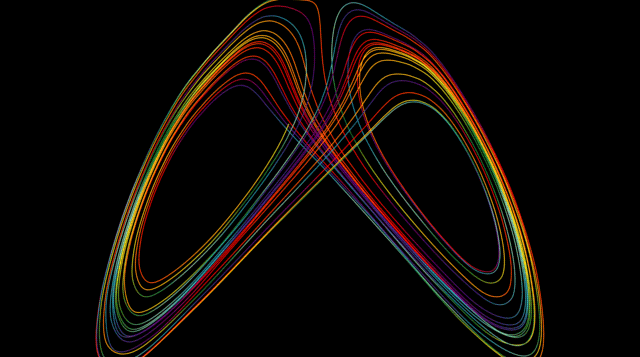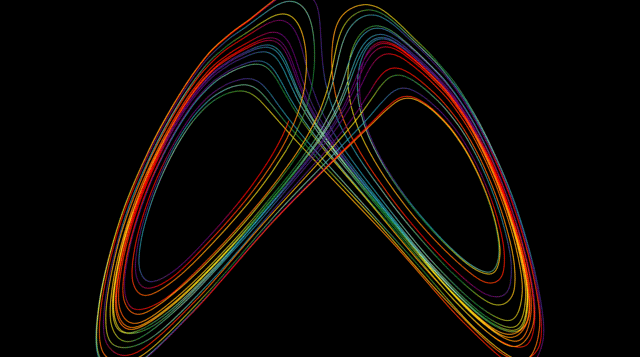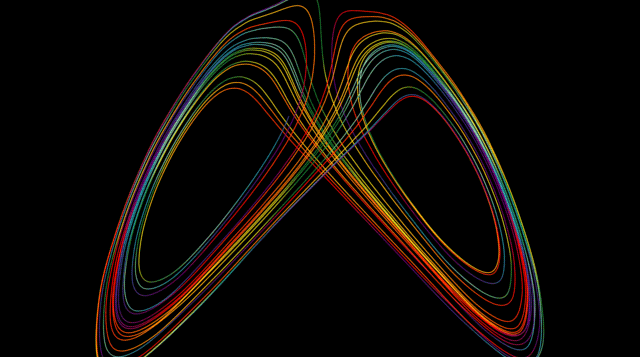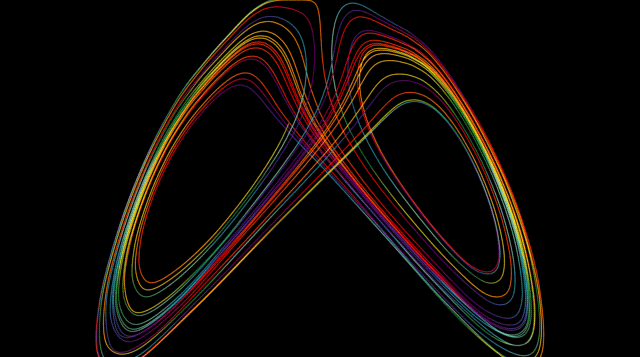
FRACTALES
Introduction
En 1975, le mathématicien belge Benoit Mandelbrot a inventé le terme Fractales pour englober ses explorations dans une nouvelle géométrie qui était "aussi rude à toutes les échelles." Son point de départ était un problème simple impliquant la mesure d'un littoral. Sur une carte à grande échelle, le littoral d'une île est très simple et les bords peuvent être représenté par une ligne droite. Pour obtenir plus de détails, il faut zoomer. La mesure à cette nouvelle échelle nécessite une règle plus petite et vous pourriez obtenir une estimation de la longueur du littoral de plus en plus précise. Cependant, alors que le calcul deviendra de plus en plus important, il sera de plus en plus difficile de distinguer le bord de la terre et celui de l'eau. Il n'y a apparement aucunes limites dans ce processus et comme nous le verrons plus loin cette approche n'a pas de limites que cela soit de l'infiniment petit à l'infiniment grand, en passant par l'économie, la biologie, la physique classique et quantique, bref cette discipline n'a pas de limites connues à ce jour.

À la fin du 19e et au début du 20e siècle, les mathématiciens ont imaginé une variété de constructions que les mathématiques de leur époques rendaient difficiles à comprendre. Par exemple avec l'ensemble de Cantor ou un ensemble infini de points obtenus en partant d'un segment de droite, ou on enlève le tiers médian (central) de la ligne, ou on enlève ensuite le tiers médian des deux morceaux restants, on enlève encore le tiers central des quatre morceaux restants, et ainsi de suite.
 |  |  |
|---|---|---|
 |  |  |
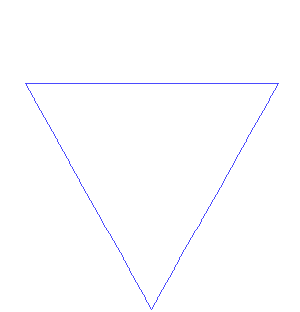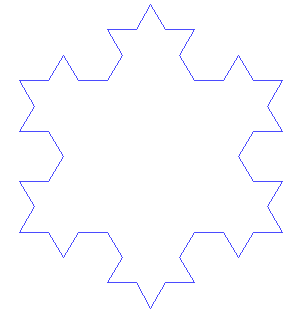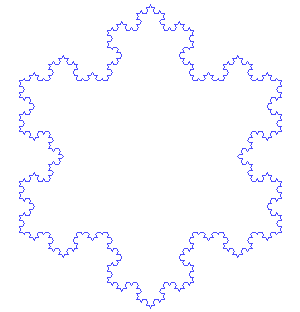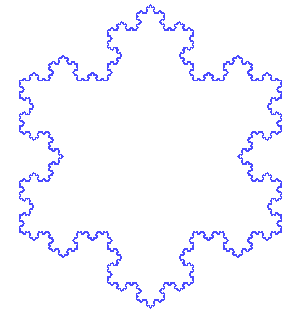
Ce processus de répétition de la même étape ou de la même série d'étapes est appelé itération et se trouve au cœur des fractales. Parmi les premiers exemples, on trouve des courbes telles que les courbes de Koch et de Peano, ainsi que le triangle de Sierpinski, qui est lié au triangle de Pascal. Dans la courbe de Koch (apparentée au flocon de neige de Koch), chaque segment de ligne droite est remplacé par quatre segments d'un tiers d'échelle à chaque itération, de sorte que la longueur de la courbe augmente à chaque itération. De tels objets sont dits de dimension fractionnaire, par exemple entre celle d'une ligne régulière et celle du plan. En appliquant l'itération à des fonctions simples telles que x 2 + c, où x et c sont des nombres complexes (ayant à la fois des parties réelles et imaginaires), et en représentant graphiquement les résultats dans le plan complexe, on obtient de beaux objets compliqués connus sous le nom d'ensembles de Julia. Benoît Mandelbrot a utilisé des ordinateurs pour visualiser ces ensembles, ainsi que l'ensemble de Mandelbrot, et a fait des fractales une branche distincte de la géométrie en mathématiques.

.png)
.png)